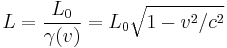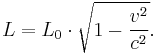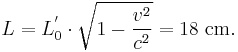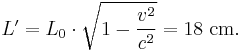Length contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer. This contraction (more formally called Lorentz contraction or Lorentz–Fitzgerald contraction) is usually only noticeable at a substantial fraction of the speed of light; the contraction is only in the direction parallel to the direction in which the observed body is travelling. This effect is negligible at everyday speeds, and can be ignored for all regular purposes. Only at greater speeds does it become important. At a speed of 13,400,000 m/s (30 million mph, .0447c), the length is 99.9% of the length at rest; at a speed of 42,300,000 m/s (95 million mph, .141c), the length is still 99%. As the magnitude of the velocity approaches the speed of light, the effect becomes dominant, as can be seen from the formula:
where
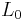 is the proper length (the length of the object in its rest frame),
is the proper length (the length of the object in its rest frame), is the length observed by an observer in relative motion with respect to the object,
is the length observed by an observer in relative motion with respect to the object,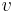 is the relative velocity between the observer and the moving object,
is the relative velocity between the observer and the moving object,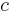 is the speed of light,
is the speed of light,
and the Lorentz factor is defined as
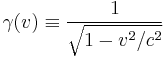 .
.
Note that in this equation it is assumed that the object is parallel with its line of movement. Also note that for the observer in relative movement, the length of the object is measured by subtracting the simultaneously measured distances of both ends of the object. For more general conversions, see the Lorentz transformations. An observer at rest viewing an object travelling very close to the speed of light would observe the length of the object in the direction of motion as very near zero.
Contents |
History
Length contraction was postulated by George Francis FitzGerald (1889) and Hendrik Antoon Lorentz (1892) to explain the negative outcome of the Michelson-Morley experiment and to rescue the hypothesis of the stationary aether (Lorentz–FitzGerald contraction hypothesis). Although both FitzGerald and Lorentz alluded to the fact that electrostatic fields in motion were deformed ("Heaviside-Ellipsoid" after Oliver Heaviside, who derived this deformation from electromagnetic theory in 1888), it was considered an Ad hoc hypothesis, because at this time there was no sufficient reason to assume that intermolecular forces behave the same way as electromagnetic ones. In 1897 Joseph Larmor developed a model in which all forces are considered as of electromagnetic origin, and length contraction appeared to be a direct consequence of this model. Yet it was shown by Henri Poincaré (1905) that electromagnetic forces alone cannot explain the electron's stability, and he had to introduce non-electric binding forces to ensure stability and to give a dynamical explanation for length contraction. But this model was subject to the same problem as the original hypotheses: Length contraction (and the non-electromagnetic forces) were only invented to hide the motion of the preferred reference frame, i.e., the stationary aether. Albert Einstein (1905) was the first who completely removed the ad-hoc character from this hypothesis, by demonstrating that length contraction was no dynamical effect in the aether, but rather a kinematic effect due to the change in the notions of space, time and simultaneity brought about by special relativity. Einstein's view was further elaborated by Hermann Minkowski and others, who demonstrated the geometrical meaning of all relativistic effects in spacetime. So length contraction is not of kinetic, but kinematic origin.[1][2][3][4][5]
Basis in relativity
First it is necessary to carefully consider the methods for measuring the lengths of resting and moving objects, where "object" simply means a distance with endpoints that are always mutually at rest, i.e., that are at rest in the same inertial frame of reference. If the relative velocity between an observer (or his measuring instruments) and the observed object is zero, then the proper length 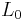 of the object can simply be determined by directly superposing a measuring rod. However, if the relative velocity > 0, then one can proceed as follows: The observer installs a row of clocks that either are synchronized a) by exchanging light signals according to the Poincaré-Einstein synchronization, or b) by "slow clock transport", that is, one clock is transported along the row of clocks in the limit of vanishing transport velocity. Now, when the synchronization process is finished, the object is moved along the clock row and every clock stores the exact time when the left or the right end of the object passes by. After that, the observer only has to look after the position of a clock A that stored the time when the left end of the object was passing by, and a clock B at which the right end of the object was passing by at the same time. It's clear that distance AB is equal to length
of the object can simply be determined by directly superposing a measuring rod. However, if the relative velocity > 0, then one can proceed as follows: The observer installs a row of clocks that either are synchronized a) by exchanging light signals according to the Poincaré-Einstein synchronization, or b) by "slow clock transport", that is, one clock is transported along the row of clocks in the limit of vanishing transport velocity. Now, when the synchronization process is finished, the object is moved along the clock row and every clock stores the exact time when the left or the right end of the object passes by. After that, the observer only has to look after the position of a clock A that stored the time when the left end of the object was passing by, and a clock B at which the right end of the object was passing by at the same time. It's clear that distance AB is equal to length  of the moving object.
of the moving object.
Thus the definition of simultaneity is crucial for measuring the length of moving objects. In Newtonian mechanics, simultaneity is absolute and therefore  and
and 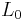 are always equal. Yet in relativity theory the constancy of light velocity in all inertial frames in connection with the relativity of simultaneity destroys this equality. So if an observer in one frame claims to have measured the object's endpoints simultaneously, the observers in all other inertial frames will argue that the object's endpoints were not measured simultaneously. The deviation between the measurements in all inertial frames is given by the Lorentz transformation. As the result of this transformation (see Derivation), the proper length remains unchanged and always denotes the greatest length of an object, yet the length of the same object as measured in another inertial frame is shorter than the proper length. This contraction only occurs in the line of motion, and can be represented by the following relation (where
are always equal. Yet in relativity theory the constancy of light velocity in all inertial frames in connection with the relativity of simultaneity destroys this equality. So if an observer in one frame claims to have measured the object's endpoints simultaneously, the observers in all other inertial frames will argue that the object's endpoints were not measured simultaneously. The deviation between the measurements in all inertial frames is given by the Lorentz transformation. As the result of this transformation (see Derivation), the proper length remains unchanged and always denotes the greatest length of an object, yet the length of the same object as measured in another inertial frame is shorter than the proper length. This contraction only occurs in the line of motion, and can be represented by the following relation (where  is the relative velocity and
is the relative velocity and  the speed of light)
the speed of light)
For example, a train at rest in S' and a station at rest in S with relative velocity of 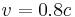 are given. In S' a rod with proper length
are given. In S' a rod with proper length 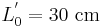 is located, so its contracted length
is located, so its contracted length 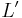 in S is given by:
in S is given by:
Then the rod will be thrown out of the train in S' and will come to rest at the station in S. Its length has to be measured again according to the methods given above, and now the proper length 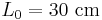 will be measured in S (the rod has become larger in that system), while in S' the rod is in motion and therefore its length is contracted (the rod has become smaller in that system):
will be measured in S (the rod has become larger in that system), while in S' the rod is in motion and therefore its length is contracted (the rod has become smaller in that system):
Thus, as it is required by the principle of relativity (according to which the laws of nature must assume the same form in all inertial reference frames), length contraction is symmetrical: If the rod is at rest in the train, it has its proper length in S' and its length is contracted in S. However, if the rod comes to rest relative to the station, it has its proper length in S and its length is contracted in S'.
Derivation
Length contraction can simply be derived from the Lorentz transformation as it was shown, among many others, by Max Born:[6]
In an inertial reference frame S', 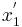 and
and 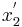 shall denote the endpoints for an object of length
shall denote the endpoints for an object of length 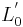 at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows:
at rest in this system. The coordinates in S' are connected to those in S by the Lorentz transformations as follows:
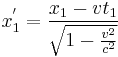 and
and 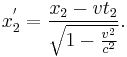
As this object is moving in S, its length  has to be measured according to the above convention by determining the simultaneous positions of its endpoints, so we have to put
has to be measured according to the above convention by determining the simultaneous positions of its endpoints, so we have to put 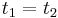 . Because
. Because 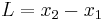 and
and 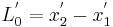 , we obtain
, we obtain
- (1)
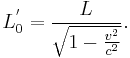
Thus the length as measured in S is given by
- (2)
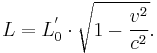
According to the relativity principle, objects that are at rest in S have to be contracted in S' as well. For this case the Lorentz transformation is as follows:
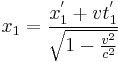 and
and 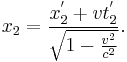
By the requirement of simultaneity 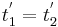 and by putting
and by putting 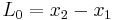 and
and 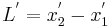 , we actually obtain:
, we actually obtain:
- (3)
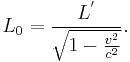
Thus its length as measured in S' is given by:
- (4)
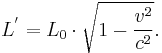
So (1), (3) give the proper length when the contracted length is known, and (2), (4) give the contracted length when the proper length is known.
Geometrical representation
-
See also: Minkowski diagram
The Lorentz transformation geometrically corresponds to a rotation in four-dimensional spacetime, and it can be illustrated by a Minkowski diagram: If a rod at rest in S' is given, then its endpoints are located upon the ct' axis and the axis parallel to it. In this frame the simultaneous (parallel to the axis of x') positions of the endpoints are O and B, thus the proper length is given by OB. But in S the simultaneous (parallel to the axis of x) positions are O and A, thus the contracted length is given by OA. On the other hand, if another rod is at rest in S, then its endpoints are located upon the ct axis and the axis parallel to it. In this frame the simultaneous (parallel to the axis of x) positions of the endpoints are O and D, thus the proper length is given by OD. But in S' the simultaneous (parallel to the axis of x') positions are O and C, thus the contracted length is given by OC.
Additional geometrical considerations show, that length contraction can be regarded as a trigonometric phenomenon, with analogy to parallel slices through a cuboid before and after a rotation in E3 (see left half figure at the right). This is the Euclidean analog of boosting a cuboid in E1,2. In the latter case, however, we can interpret the boosted cuboid as the world slab of a moving plate.
In special relativity, Poincaré transformations are a class of affine transformations which can be characterized as the transformations between alternative Cartesian coordinate charts on Minkowski spacetime corresponding to alternative states of inertial motion (and different choices of an origin). Lorentz transformations are Poincaré transformations which are linear transformations (preserve the origin). Lorentz transformations play the same role in Minkowski geometry (the Lorentz group forms the isotropy group of the self-isometries of the spacetime) which are played by rotations in euclidean geometry. Indeed, special relativity largely comes down to studying a kind of noneuclidean trigonometry in Minkowski spacetime, as suggested by the following table:[A 1]
Experimental verifications
Since the occurrence of length contraction depends on the inertial frame chosen, it can only be measured by an observer not at rest in the same inertial frame, i.e., it exists only in a non-co-moving frame. This is because the effect vanishes after a Lorentz transformation into the rest frame of the object, where a co-moving observer can judge himself and the object as at rest in the same inertial frame in accordance with the relativity principle (as it was demonstrated by the Trouton-Rankine experiment). In addition, even in a non-co-moving frame, direct experimental confirmations of Lorentz contraction are hard to achieve, because at the current sate of technology, objects of considerable extension cannot be accelerated to relativistic speeds. And the only objects traveling with the speed required are atomic particles, yet whose spatial extensions are too small to allow a direct measurement of contraction.
However, there are indirect confirmations of this effect in a non-co-moving frame. It was in fact the negative result of a famous experiment, that required the introduction of Lorentz contraction: the Michelson-Morley experiment (and later also the Kennedy–Thorndike experiment). In special relativity its explanation is as follows: In its rest frame the interferometer can be regarded as at rest in accordance with the relativity principle, so the propagation time of light is the same in all directions. However, in a frame in which the interferometer is in motion, the propagation time of the transverse beam is time dilated, while in the longitudinal direction the interferometer is also contracted, so that speed of light is constant and the propagation time in both directions is the same in this frame as well.
Other indirect confirmations are: Heavy ions that are spherical when at rest should assume the form of "pancakes" or flat disks when traveling nearly at the speed of light. And in fact, the results obtained from particle collisions can only be explained, when the increased nucleon density due to Lorentz contraction is considered.[7][8][9][10] Another confirmation is the increased ionization ability of electrically charged particles in motion. According to pre-relativistic physics the ability should decrease at high speed, however, the Lorentz contraction of the Coulomb field leads to an increase of the electrical field strength normal to the line of motion, which leads to the actually observed increase of the ionization ability.[11] Lorentz contraction is also necessary to understand the function of free-electron lasers. Relativistic electrons were injected into an undulator, so that synchrotron radiation is generated. In the proper frame of the electrons, the undulator is contracted which leads to an increased radiation frequency. Additionally, to find out the frequency as measured in the laboratory frame, one has to apply the relativistic Doppler effect. So, only with the aid of Lorentz contraction and the rel. Doppler effect, the extremely small wavelength of undulator radiation can be explained.[12][13] Another example is the observed lifetime of muons in motion and thus their range of action, which is much higher than that of muons at low velocities. In the proper frame of the atmosphere, this is explained by the time dilation of the moving muons. However, in the proper frame of the muons their lifetime is unchanged, but the atmosphere is contracted so that even their small range is sufficient to reach the surface of earth.[11]
Reality of Lorentz contraction
Another issue that is sometimes discussed concerns the question whether this contraction is "real" or "apparent". However, this problem only stems from terminology, as our common language attributes different meanings to both of them. On one side, the word "real" is used for things that we can measure without considerable observational errors, and "apparent" therefore denotes to the products of observational error, optical distortions, or displaced images like a Fata Morgana. If this definition is chosen, length contraction would be "real" since it principally can be detected by error free measurements of the simultaneous positions of the object's endpoints, and also by measuring its consequences (see the section "experimental verifications"). On the other side, "real" is also used in connection with "absolute", and "apparent" is thus "relative". This is related to the principle of relativity, according to which any inertially moving observer can consider himself as at rest, and attribute the motion to the other observers. If this definition is chosen, length contraction would be "apparent" since it depends on the inertial motion of bodies. Yet, whatever terminology is chosen, in physics the measurement and the consequences of length contraction with respect to any reference frame are clearly and unambiguously defined in the way stated above.[14]
Paradoxes
Due to superficial application of the contraction formula some paradoxes can occur. For examples see the Ladder paradox or Bell's spaceship paradox. However, those paradoxes can simply be solved by a correct application of relativity of simultaneity. Another famous paradox is the Ehrenfest paradox, which proves that the concept of rigid bodies is not compatible with relativity. It also shows that for a co-rotating observer the geometry is in fact non-euclidean.
Visual effects
Length contraction refers to measurements of position made at simultaneous times according to a coordinate system. This could naively lead to a thinking that if one could take a picture of a fast moving object, that the image would show the object contracted in the direction of motion. However, it is important to realize that such visual effects are completely different measurements, as such a photography is taken from a distance, while length contraction can only directly be measured at the exact location of the object's endpoints. In 1959 Roger Penrose and James Terrell published papers demonstrating that length contraction instead actually show up as elongation or even a rotation in an image of photography.[15][16][17] This kind of visual rotation effect is called Penrose-Terrell rotation.[18]
See also
- Time dilation
- Ehrenfest paradox
- Ladder paradox
- Lorentz transformation
- Relativity of simultaneity
- Kennedy–Thorndike experiment
- Trouton–Rankine experiment
- Michelson–Morley experiment
Notes
- ^
Three plane trigonometries Trigonometry Circular Parabolic Hyperbolic Kleinian Geometry euclidean plane Galilean plane Minkowski plane Symbol E2 E0,1 E1,1 Quadratic form positive definite degenerate non-degenerate but indefinite Isometry group E(2) E(0,1) E(1,1) Isotropy group SO(2) SO(0,1) SO(1,1) type of isotropy rotations shears boosts Cayley algebra complex numbers dual numbers split-complex numbers ε2 -1 0 1 Spacetime interpretation none Newtonian spacetime Minkowski spacetime slope tan φ = m tanp φ = u tanh φ = v "cosine" cos φ = (1+m2)-1/2 cosp φ = 1 cosh φ = (1-v2)-1/2 "sine" sin φ = m (1+m2)-1/2 sinp φ = u sinh φ = v (1-v2)-1/2 "secant" sec φ = (1+m2)1/2 secp φ = 1 sech φ = (1-v2)1/2 "cosecant" csc φ = m−1 (1+m2)1/2 cscp φ = u−1 csch φ = v−1 (1-v2)1/2
References
- ^ FitzGerald, George Francis (1889), "The Ether and the Earth's Atmosphere", Science 13 (328): 390, Bibcode 1889Sci....13..390F, doi:10.1126/science.ns-13.328.390, PMID 17819387
- ^ Lorentz, Hendrik Antoon (1892), "The Relative Motion of the Earth and the Aether", Zittingsverlag Akad. V. Wet. 1: 74–79
- ^ Einstein, Albert (1905), "On the Electrodynamics of Moving Bodies", Annalen der Physik 322 (10): 891–921, Bibcode 1905AnP...322..891E, doi:10.1002/andp.19053221004.
- ^ Janssen, Michel H. P. (2007), "Drawing the line between kinematics and dynamics in special relativity", Symposium on Time and Relativity: 1–76, http://philsci-archive.pitt.edu/3895/
- ^ Torretti, Roberto (2006), "Can science advance effectively through philosophical criticism and reflection?", [no journal title given]: 1–84, http://philsci-archive.pitt.edu/2875/
- ^ Born, Max (1964), Einstein's Theory of Relativity, Dover Publications, ISBN 0486607690
- ^ The Physics of RHIC
- ^ Relativistic heavy ion collisions
- ^ GSI: Heavy-ion induced electromagnetic interactions
- ^ Simon Hands, The Phase Diagram of QCD, Contemp. Phys. 42:209-225, 2001, arXiv:physics/0105022
- ^ a b Sexl, Roman & Schmidt, Herbert K. (1979), Raum-Zeit-Relativität, Braunschweig: Vieweg, ISBN 3528172363
- ^ http://hasylab.desy.de/science/studentsteaching/primers/synchrotron_radiation/index_eng.html
- ^ FLASH The Free-Electron Laser in Hamburg (PDF 7.8MB)
- ^ See for example Physics FAQ: "People sometimes argue over whether the Lorentz-Fitzgerald contraction is "real" or not... here's a short answer: the contraction can be measured, but the measurement is frame dependent. Whether that makes it "real" or not has more to do with your choice of words than the physics."
- ^ Terrell, James (1959), Invisibility of the Lorentz Contraction, http://www.guspepper.net/electro/Segundo%20semestre/Seminarios/Funez.pdf, Phys. Rev. 116, 1041 - 1045 (1959)
- ^ Roger Penrose (1959), "The Apparent shape of a relativistically moving sphere", Proc.Cambridge Phil.Soc.55:137-139,1959. url=http://journals.cambridge.org/production/action/cjoGetFulltext?fulltextid=2117060
- ^ Penrose, Roger (2005). The Road to Reality. London: Vintage Books. pp. 430-431. ISBN 978-0-099-44068-0.
- ^ Can You See the Lorentz-Fitzgerald Contraction? Or: Penrose-Terrell Rotation